SCT Topic 8: Password Cracking

Case Study: Adobe Password Leak

If you are familiar with how online service store users’s password, let me ask you:

How Should You Do?

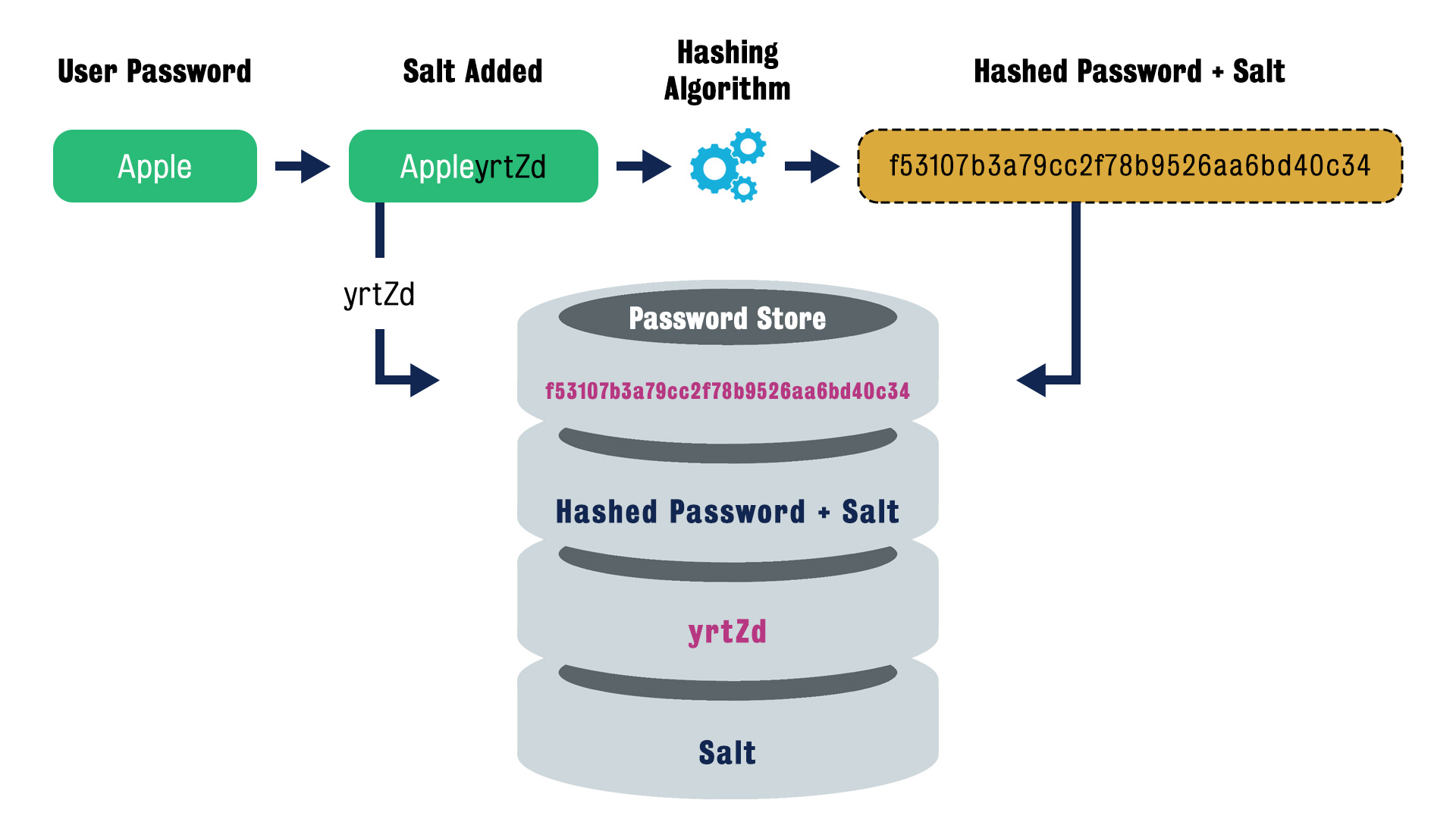
Yes, we will use hash algorithm, salt and store the hashed password and salt, which actively avoid the exposion of plaintext password and brute force.

But how Adobe Did It?

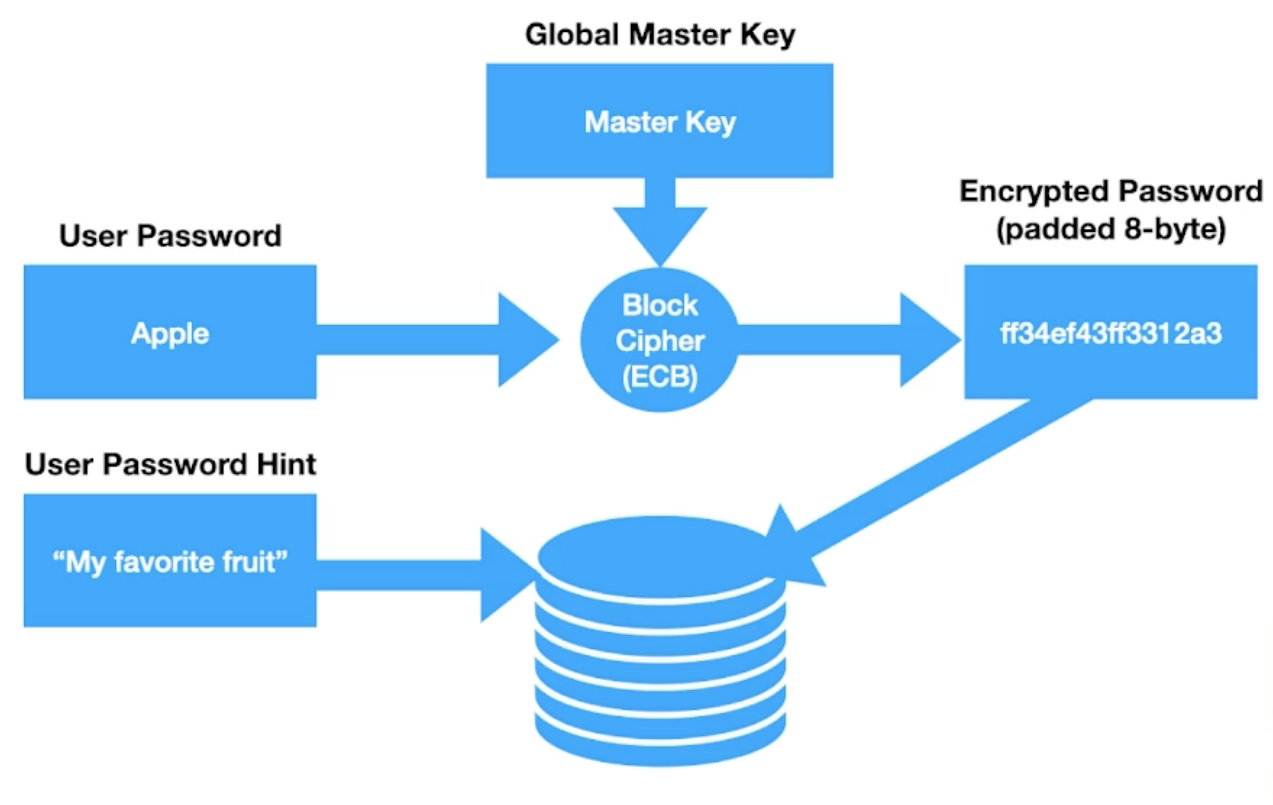
What were the consequences?

If you get the master key, literally you own all “encrypted passwords”
If two users choose same password, their encrypted ciphertext are same, consequently, frequently analysis would help hacker to find out the details of encryption process.

For more details, please refer to this article: Anatomy of a password disaster – Adobe’s giant-sized cryptographic blunder

Cryptanalysis basics

Cryptanalysis: The study of techniques to reveal what cryptography is attempting to hide or protect.

In other words, break the cryptographyic algorithms without knowing the key.

Cryptanalysis are based on:

The nature of the cryptographic algorithm
the key
some knowledge on the text, such as language(common words), format or encoding (script, image alway begin with some same pattern),
a section with both plaintext and encrypted text

Brute-force attacks

Brute-force attack: Aim to decrypt an encrypted text by exhaustively trying all possible secret keys until you obtain a meaningful plaintext

On average, you need to try at least half of all the possible keys to be successful

For example, to brute force a 4-digit password, the number of possibilities is 10^4 = 10000, therefore, on average, a brute-force attack in this scenario will succeed after 5000 attempts. If 1 attempt cost 1s, it needs at least 1h24min to finish this work.

Dictionary attacks

4-digit password needs one hour and half? Forget about it, let’s to try something not so naive.

Let’s first define the term “password” as a user-defined encrypted secret key.

Passowrd dictionary attacks: Use a “dictionary” of possbile words (based on an attacker-defined alphabet) to make exploitation attempts, including English words, user’s private information and common passwords.

Common dictionaries for attacks include:

Words and meaningful fragments of words combination for a certain language
Personal information (e.g., obtained from OSINT or social engineering)
Lists of names, locations, dates, companies, etc.

Therefore, if the attackers use dictionary attack, the password length does not provide too much help on password robustness.

Password robustness

There are four main elements to determine the security of a password

Number of symbols in the password

As we mentioned before, 4-digit locker would require on average 10^4/2 seconds, or almost 1.5 hours to brute force, the longer password, the longer time to brute force.

Number of possibilities for each position

We continue use previous example, if we expand the types of symbols to alphabet and number, the possibilities expand to 36*36*36 for brute force, which requires much more time than 1.5 hours.

Time required for each attempt

Based on my experience, some online service will delay the login attempt to expand the time of brute force, which may also help to defend the attack like DDoS.

Are there easier alternatives

Remember we metioned in Social Engineering: “The easiest way to get the information you want is always by asking the victims themselves”?

There are always more than one way to get the answer of a question, so does cryptanalysis, you can even physically break the lock :)

Some common alternatives:

finding write-down notes in officers
shoulder-surfing, i.e., looking over someone’s shoulder when they’re typing their passwords
physical break-in
physically stealing passwords lists or logbooks

Cryptographic hash functions

Hash function

A function that maps input data of arbitrary size to fixed-size output values called hashes.

Crytographic hash functions (CHF)

are hash functions more suitable for information security applications which contains ideal following properties:

deterministic: given message M, its hash H(M) is always the same
quick to compute
unfeasible to generate message M that has a specific hash value H (hard to find alternative message M')
unfeasible to find messages M1 and M2 such that H(M1) = H(M2) (hard to find a collision)
avalanche effect: a small change in message M leads to siginificant change to the hash value.

Usage of CHF includes MACs (Message Authentication Codes), digital signatures and authentications.

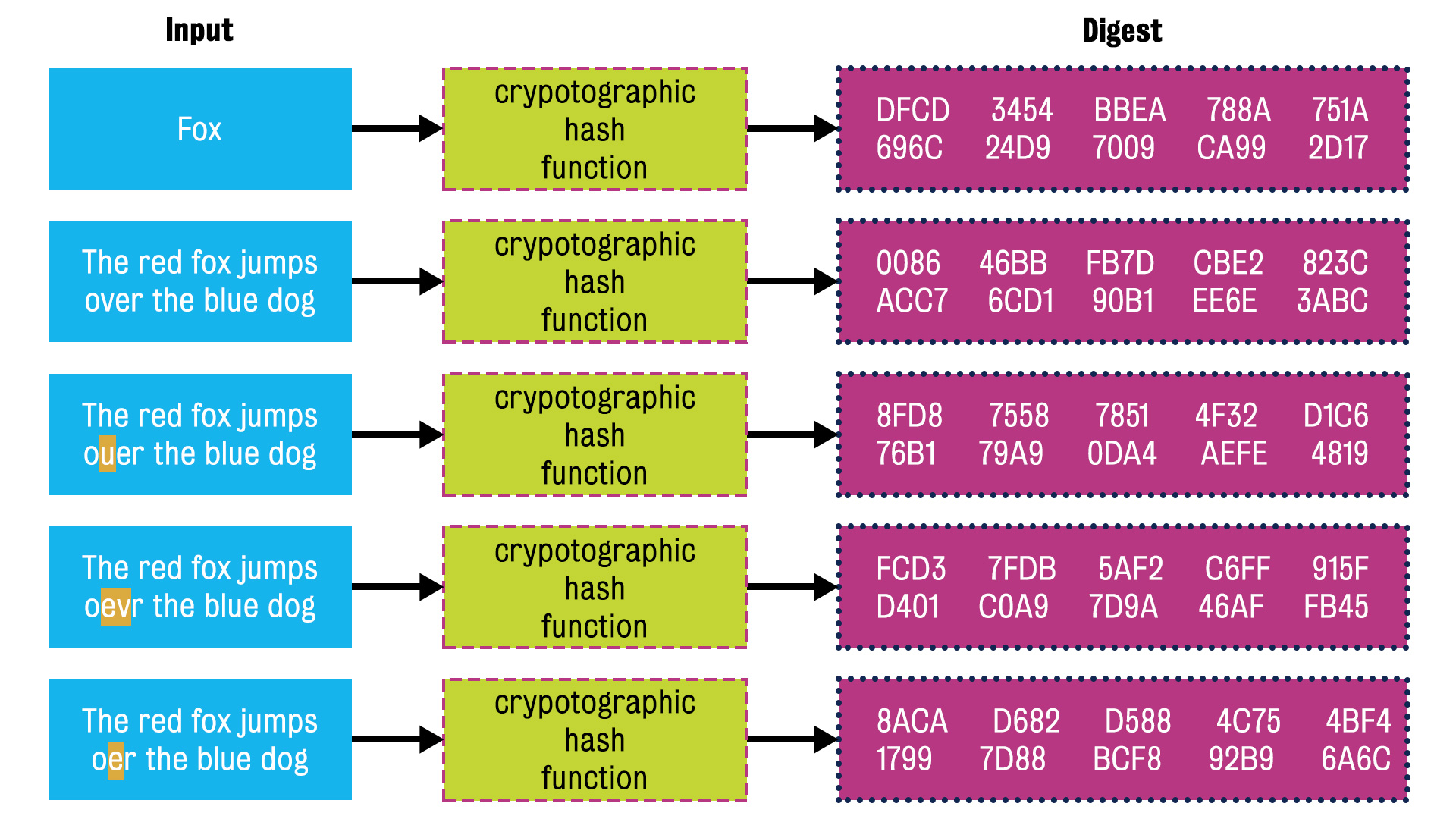
Let’s use an example for better understanding of CHF

Left hand column is the input, after cryptographic hash function, we get the output, we called Digest here.

We can observe that, a single character change of input text, the digest would be very different from previous one.

As you can easily guess, there are many problems and attacks which threat the CHF:

The birthday problem (or the birthday paradox)

Let me ask you a classic question, how many people you need in a single room, which makes the probability that at least two person share a birthday to be 50%?

You only need 23 people to raise probability to 50 per cent.

Prove: The goal is to compute P(A), the probability that at least two people in the room have same birthday.

However, it is simpler to calculate the reverse one, P(A’), the probability that NO two people in the room have the same birthday.

To calculate P(A’), the event is that person 2 does not have the same birthday as person 1, and that persona 3 does not have the same birthday as either person 1 or person 2, and so on, and finally that person 23 does not have the same birthday as any of persons 1 through 22.

Let’s number this event as Event 1 to Event 23

Let’s calculate the product of the probability of these events:

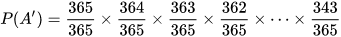
Evaluating equation with (23) gives P(A’) ≈ 0.492703

Therefore, P(A) ≈ 1 − 0.492703 = 0.507297 (50.7297%).

Also, according to the pigenhole principle, the probability reaches 100 per cent when at least 367 people are present since there are only 366 possible birthdays.

Based on above knowledge, we can understand that birthday attack is based on higher likelihood of collisions found between random attack and fixed degree of permutations.

Collision attack

The collision attack aims to identify two inputs that generate the same hash.

More formally, we assume user has password P with hash H(P), an attacker may find another string Q, such that H(P) = H(Q)

This is why we need CHF to have the property to make it feasible to find the collision.

Preimage attack

The preimage attack aims to find a message that has a specific hash value

More formally, an adversary “tweaks” an input message M’ until H(M’)=H(M)

This attack will put huge harm to the security property: Integrity, because if this kind of tweak success, we can not trust anything, even if it has been hashed.

Let’s see an example:

Message M: Give Mr John Smith a salary increase of £1,000.

This message will be digitally signed as a contract by CHF H.

But the attacker finds some alternatives of messages which change their meaning of the input message, but get the same output digest as H(M)

Message M’: Award Mr Smith a raise of £2,000
Message M’’: Present John Smith a bonus of £3,000

Same signed hash value, different meaning, how powerful it is…

MD5 collision exercise

When we download some files/software, many of them will provide md5 authentication, to authenticate that the integrity of the software, however, here is a exercise that shows MD5 can not be trusted anymore.

Please review the details, I will just post something interesting here:

Let’s see two programs like this:

Program 1: if (data1 == data1) then { good_program } else { evil_program }
Program 2: if (data2 == data1) then { good_program } else { evil_program }

The only difference between these two statements is the variable to compare, however, it has been proved by Chinese researchers that we can only change some data in the input source files, but get the same MD5 hash value, which announce the death of MD5.

Rainbow table attacks

In this section, we will see a smarter variant of dictionary attack to do the brute force, it called pre-computed dictionary attack.

In this attack, we will pre-compute a list of hashes of dictionary words, and store in a table, which you can always easily to map the hashed text and plaintext password. If “hash-chain” functions are used to store the pre-computed hashes(to reduce the storage space), then the table is called a rainbow table.

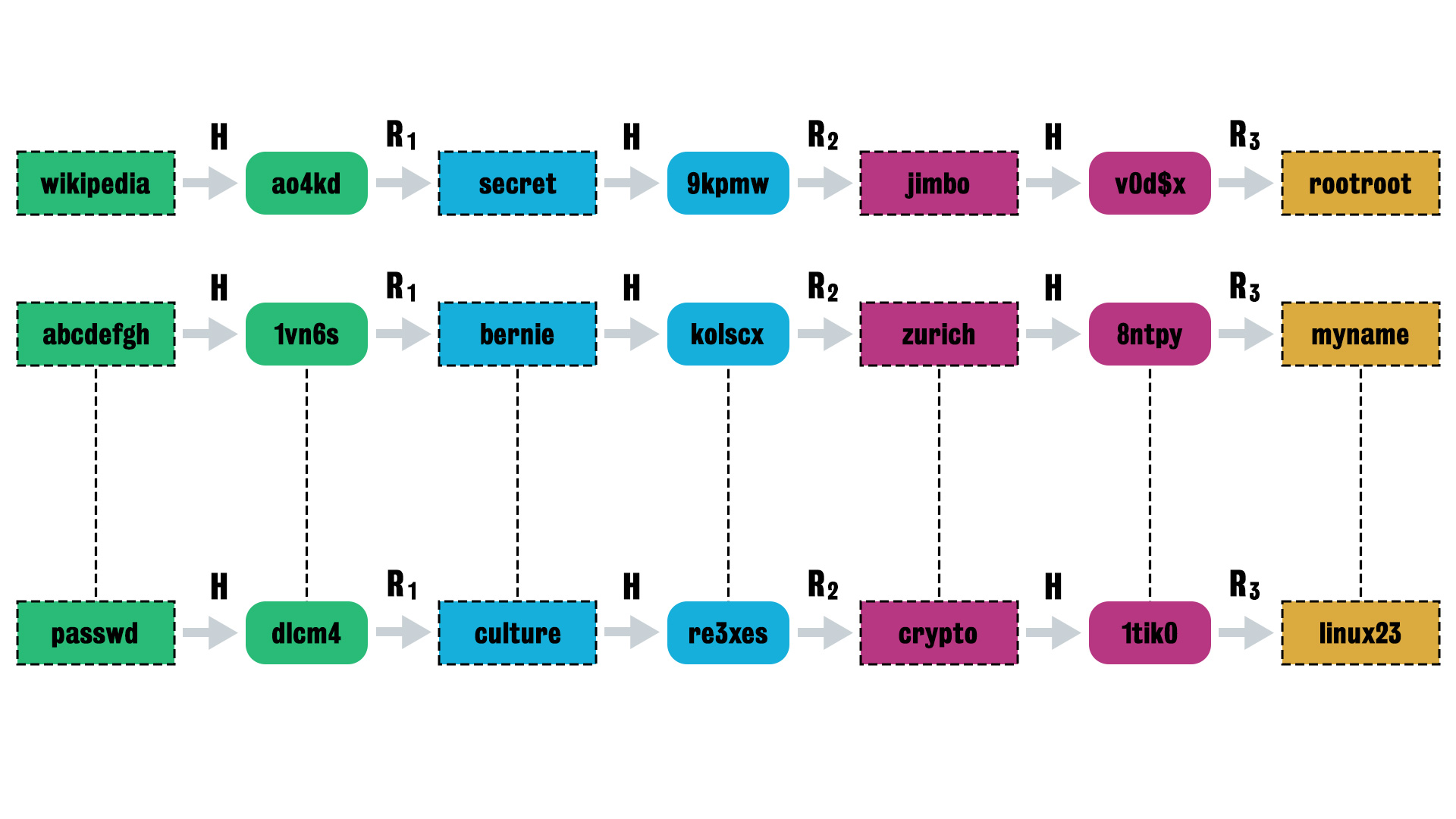
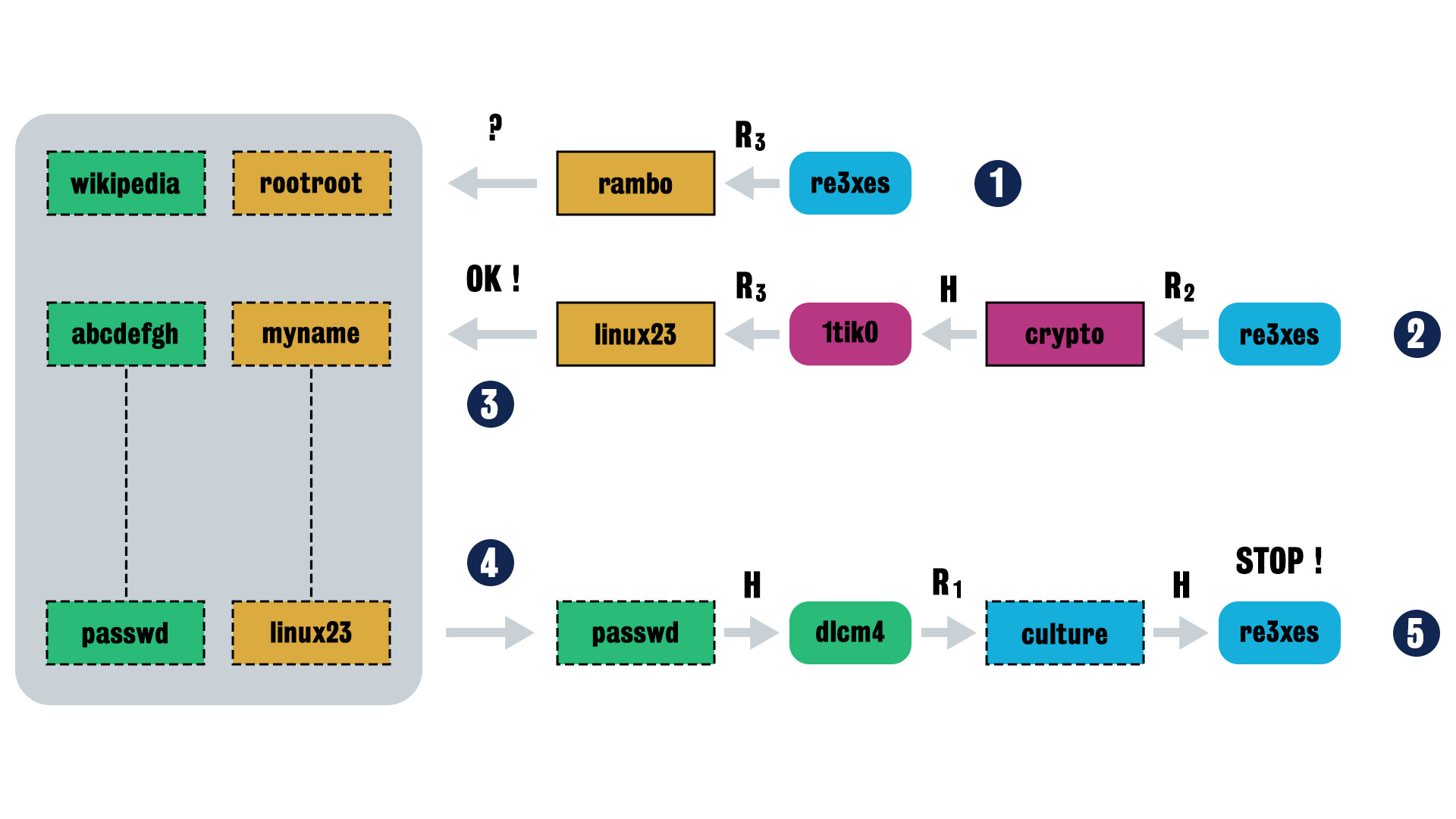
Let’s use an example to introduce the terms and processes in a Rainbow Table usage.

The letter H denotes a hash function.
The letters R_i denote different reduction functions, which aim to store more plaintext-hashed-text chains in the table (The number and sequences of reduction functions are same in each row).

We only store two columns of data in a system: 1. The first column (in green) and the last (in yellow).

How we utilise the rainbow table the plaintext of a given hashed text?

Step 0 We find the hashed text "re3xes" in /etc/shadow directory of the victim, we want the plaintext of this password, and have a rainbow table which contains two columns (green and yellow).

Step 1 We use the reduction function R3 on "re3xes" (start from last reduction function) and see if the result “rambo” is in the last column of the rainbow table. In this example it is not.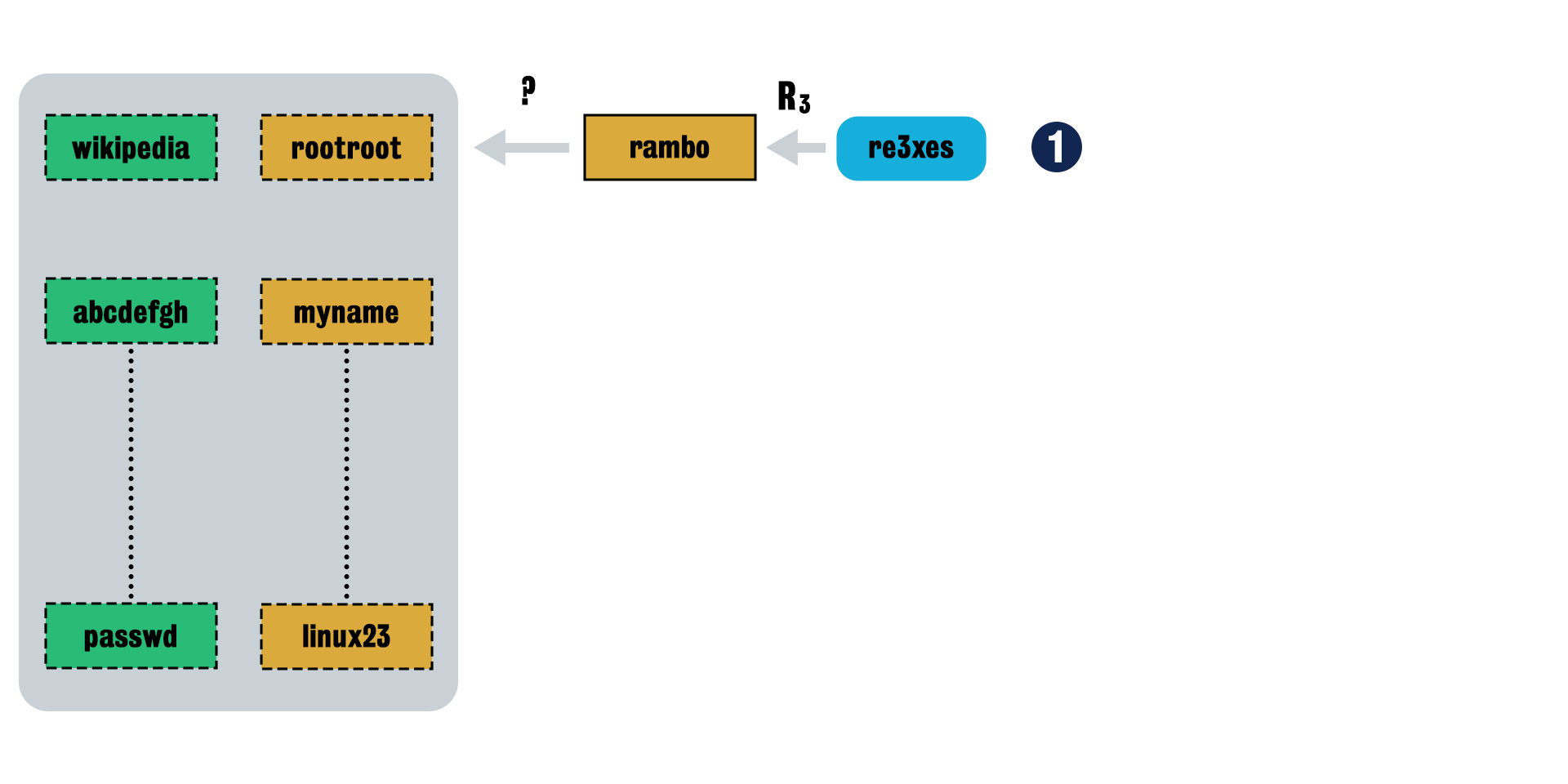
Step 2 Next, try two rounds of reduction function, use reductions R2 and R3 and obtain “linux23” as the result.
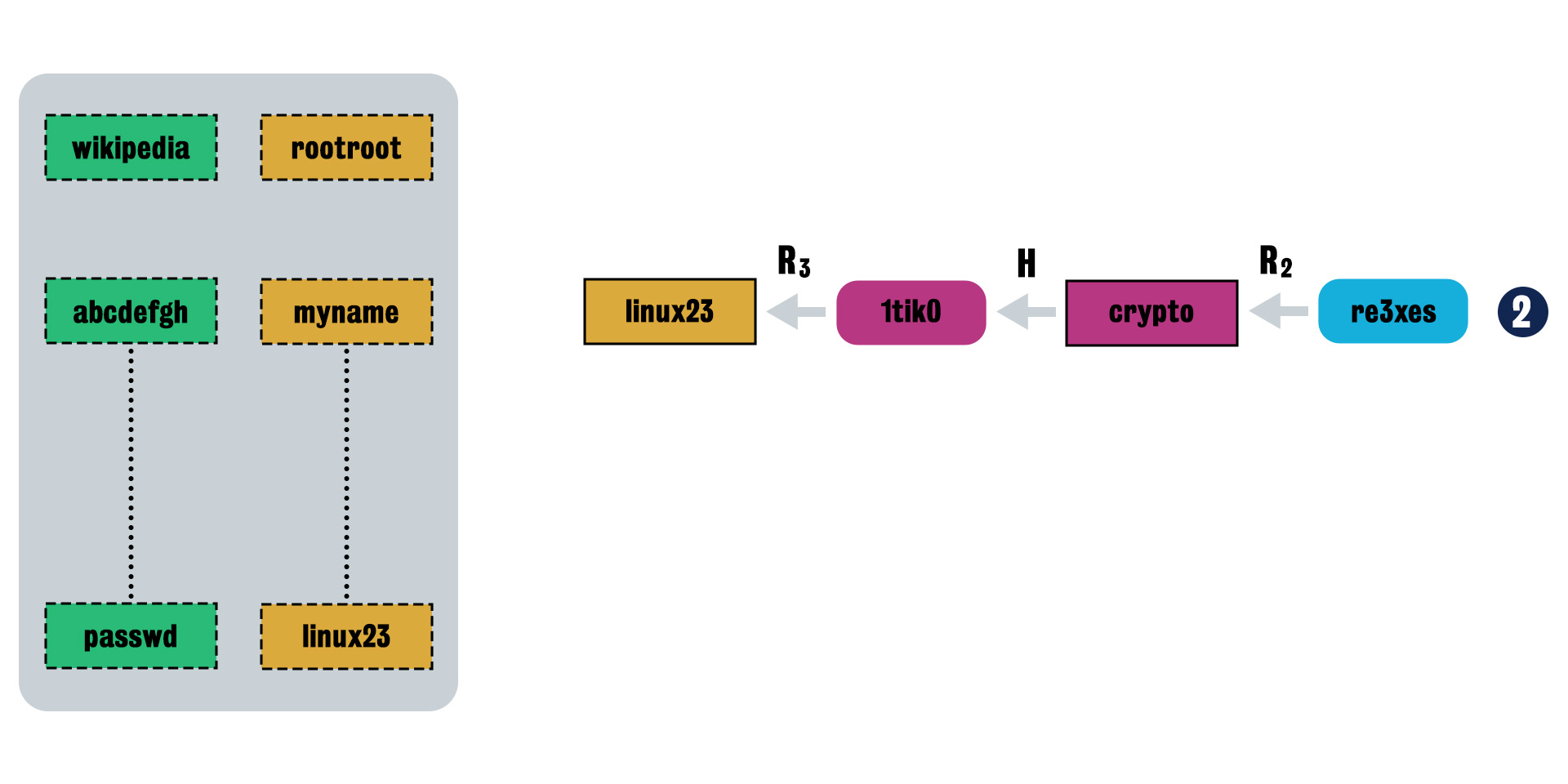
Step 3 Find the match
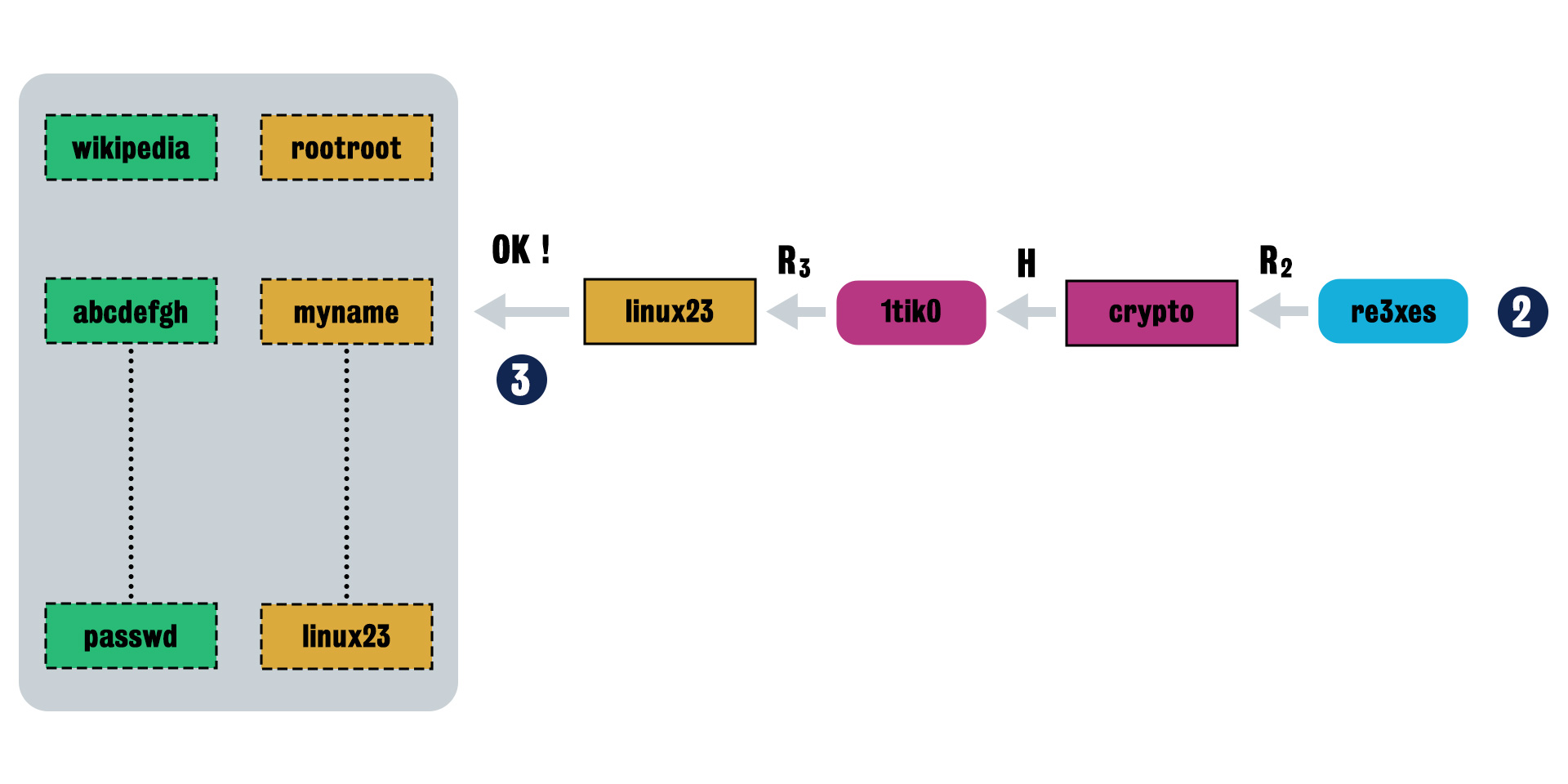
Step 4 Start with matched plaintext column “passwd” and do the reductions to reach plaintext which will hashed to given hashed text “re3xes”.

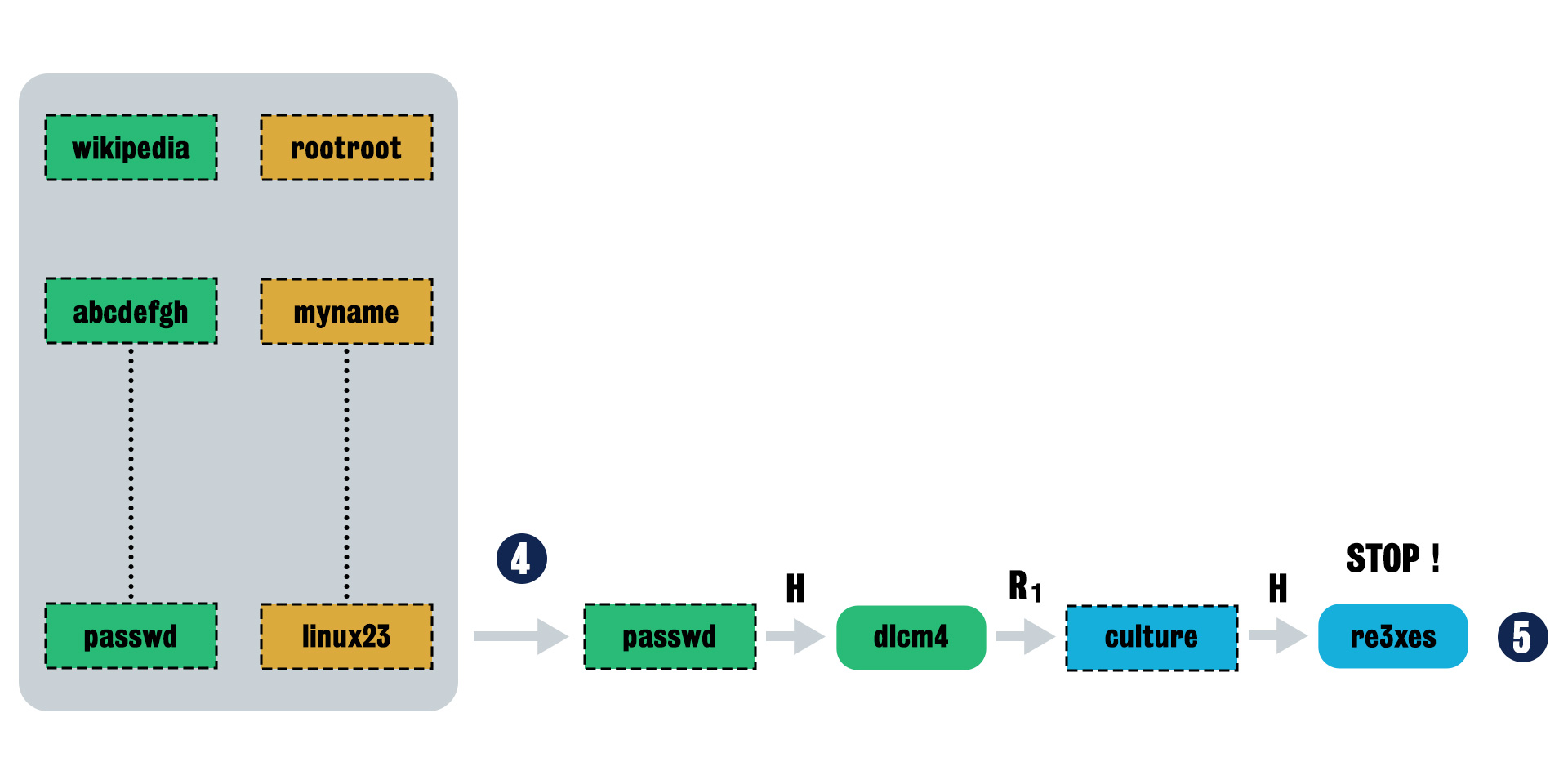
Summary: We assume that the given hashed text are contained in the chains of a row in the rainbow table, and use a sequence of reduction functions and hash function to see if it could reach the last column.
If there is match, then we could locate the row of first (green) column and begin to reproduce the chains and get the plaintext.

Salt

Remember that I mentioned a term in first section: Salt?

Rainbow table attacks and pre-computed dictionary attacks can be thwarted via the use of salt.

The reason is very simple, even if you can use pre-computed table based on some common use dictionaries, but you can predict what’s the salt are used in hashing.

Here are the most common mistakes in applying salt:

Using short salts: if the salt is too short, the attacker may predict or brute-force pre-computed dictionaries with known salts.
Reusing salts: if you reuse the salt for multiple accounts, the attacker can easily find out that the plaintext passwords were the same, and use side-channel information (e.g., password hints) to corrupt multiple accounts at once.

Moreover, if the attacker randomly predicted the correct salt while computing a precomputed dicionary, then all the passwords would be compromised at once.

Finally it is important to note that using a ‘salt’ is not robust enough to thwart dictionary attacks, but only the pre-computation.

Countermeasures and best practices

Weak passwords

Default passwords

Default provided by system vendor which should be changed at installation time

password
default
admin
guest

Dictionary words

Including non-English dictionaries:

chameleon
RedSox
sandbags
bunnyhop
IntenseCrabtree

Words with numbers appended

These can be easily tested automatically by attackers with little time cost.

password1
deer2000
john1234

Words with simple obfuscations

Still, it can be tested automatically with little additional effort

p@ssw0rd
l33th4x0r
g0ldf1sh

Doubled words

crabcrab
stopstop
treetree
passpass.

Common sequences from a keyboard row

qwerty (keyboard)
123456
asdfgh (keyboard)
fred.

Numeric sequences based on well known numbers such as

911 (9-1-1, 9/11)
314159… (pi)
27182… (e)
112 (1-1-2).

Identifiers

jsmith123
1/1/1970
555–1234
one’s username.

Weak passwords in non-English languages

contraseña (Spanish)
ji32k7au4a83 (encoding from Chinese).

Anything personally related to an individual

All these can be easily tested automatically after a simple investigation of a person’s details, eg through social engineering.

license plate number
social security number
current or past telephone numbers
student ID number
current address
previous addresses
birthday
sports team
relative’s or pet’s names, nicknames, birthdays, initials, etc.

Dates

Dates follow a pattern and make passwords weak.

Common passwords from previous leaks

For example, the top 10 most common passwords in a CNN article:

123456
123456789
qwerty
password
111111
12345678
abc123
1234567
password1

Side-channel attacks

As its name suggest, rather than exploiting the weakness of the algorithm itself (eg. cryptanalysis and software bugs), a side-channel attack relies on information gained from the implementation of a computer system.

For example:

timing information (eg, implement the encryption, hashing)
power consumption
electromagnetic leaks
sound

If you are familar with SQL injection, the time-based blind injection is also a side-channel attacks.

Let’s look at the details of a timeing attack: By analyse time taken by the cryptographic algorithm implementation operation, the attacker is able to reverse engineer the input.

In 2003, Boneh and Brumley published a practical network-based timing attack on SSL-enabled web server, the server key was recovered in a matter of hours using this method.

Good practice around passwords

Do not reuse passwords
- Browser
- KeePassX
- Local
Use password managers
Use Two-Factor Authentication (2FA)